13.9. From Serial to Parallel (Parallel TetOpSplit Solver)

The simulation script described in this chapter is available at STEPS_Example repository.

The TetOpSplit solver is avialble for STEPS 3.0.0 and above. Please note that the solver is still under active development and some of the functionaliies are not yet available or with limited support. Here is the feature status of solver:

• Fully Supported

  • Non-interactive parallel stochastic spatial reaction-difusion-EField simulation (similar to Tetexact)

• Not Yet Supported

  • Checkpointing

  • dynamic load balancing

  • Simulation visualization

For more details about the accuracy and performace of the parallel TetOpSplit solver, please check the following papers:

Hepburn, I., Chen, W., and De Schutter, E. (2016). Accurate reaction-diffusion operator splitting on tetrahedral meshes for parallel stochastic molecular simulations. J. Chem. Phys. 145, 054118–22. doi:10.1063/1.4960034.

Chen W and De Schutter E (2017). Parallel STEPS: Large Scale Stochastic Spatial Reaction-Diffusion Simulation with High Performance Computers. Front. Neuroinform. 11:13. doi: 10.3389/fninf.2017.00013.

13.9.1. Reaction-Diffusion Simulation

Let’s first see how to convert a normal serial Tetexact reaction-diffusion simulation to a parallel TetOpSplit simulation. Below is the Tetexact simulation script,

#  This script is provided as example for STEPS user manual.
#  License: GPL2.0
#  Contact: Dr. Weiliang Chen, w.chen@oist.jp

import os
import time

import steps.geom as stetmesh
import steps.model as smod
import steps.rng as srng
import steps.solver as ssa_solver
import steps.utilities.meshio as meshio

dirPath = os.path.dirname(os.path.abspath(__file__))
MESHFILE = os.path.join(dirPath, '../../meshes/parallel/10x10x100_3363tets.inp')
RESULT_DIR = os.path.join(dirPath, "serial_result")

#  The initial molecule counts
N0A = 1000
N0B = 2000
N0C = 3000
N0D = 4000
N0E = 5000
N0F = 6000
N0G = 7000
N0H = 8000
N0I = 9000
N0J = 10000

ENDTIME = 20.0
RECORDING_INTERVAL = 1.0

########################################################################
#  Biochemical Model


def gen_model():

    mdl = smod.Model()

    # The chemical species
    A = smod.Spec('A', mdl)
    B = smod.Spec('B', mdl)
    C = smod.Spec('C', mdl)
    D = smod.Spec('D', mdl)
    E = smod.Spec('E', mdl)
    F = smod.Spec('F', mdl)
    G = smod.Spec('G', mdl)
    H = smod.Spec('H', mdl)
    I = smod.Spec('I', mdl)
    J = smod.Spec('J', mdl)

    volsys = smod.Volsys('vsys', mdl)

    R1 = smod.Reac('R1', volsys, lhs=[A, B], rhs=[C], kcst=1000.0e6)
    R2 = smod.Reac('R2', volsys, lhs=[C], rhs=[A, B], kcst=100)
    R3 = smod.Reac('R3', volsys, lhs=[C, D], rhs=[E], kcst=100e6)
    R4 = smod.Reac('R4', volsys, lhs=[E], rhs=[C, D], kcst=10)

    R5 = smod.Reac('R5', volsys, lhs=[F, G], rhs=[H], kcst=10e6)
    R6 = smod.Reac('R6', volsys, lhs=[H], rhs=[F, G], kcst=1)
    R7 = smod.Reac('R7', volsys, lhs=[H, I], rhs=[J], kcst=1e6)
    R8 = smod.Reac('R8', volsys, lhs=[J], rhs=[H, I], kcst=0.1 * 10)

    # The diffusion rules
    D1 = smod.Diff('D1', volsys, A, 100e-12)
    D2 = smod.Diff('D2', volsys, B, 90e-12)
    D3 = smod.Diff('D3', volsys, C, 80e-12)
    D4 = smod.Diff('D4', volsys, D, 70e-12)
    D5 = smod.Diff('D5', volsys, E, 60e-12)
    D6 = smod.Diff('D6', volsys, F, 50e-12)
    D7 = smod.Diff('D7', volsys, G, 40e-12)
    D8 = smod.Diff('D8', volsys, H, 30e-12)
    D9 = smod.Diff('D9', volsys, I, 20e-12)
    D10 = smod.Diff('D10', volsys, J, 10e-12)

    return mdl


########################################################################
#  Geometry
def gen_geom():
    mesh = meshio.importAbaqus(MESHFILE, 1e-6)[0]
    ntets = mesh.countTets()
    comp = stetmesh.TmComp('comp', mesh, range(ntets))
    comp.addVolsys('vsys')

    return mesh


########################################################################

m = gen_model()
g = gen_geom()

########################################################################
#  recording

try:
    os.mkdir(RESULT_DIR)
except:
    pass

summary_file = open(RESULT_DIR + "/result.csv", 'w', 1)
summary_file.write("Simulation Time,A,B,C,D,E,F,G,H,I,J\n")

########################################################################

rng = srng.create('mt19937', 512)
rng.initialize(int(time.time() % 4294967295))

sim = ssa_solver.Tetexact(m, g, rng)


#  Set initial conditions
sim.setCompCount('comp', 'A', N0A)
sim.setCompCount('comp', 'B', N0B)
sim.setCompCount('comp', 'C', N0C)
sim.setCompCount('comp', 'D', N0D)
sim.setCompCount('comp', 'E', N0E)
sim.setCompCount('comp', 'F', N0F)
sim.setCompCount('comp', 'G', N0G)
sim.setCompCount('comp', 'H', N0H)
sim.setCompCount('comp', 'I', N0I)
sim.setCompCount('comp', 'J', N0J)

n_tpns = int(ENDTIME / RECORDING_INTERVAL) + 1

for l in range(n_tpns):
    sim_endtime = RECORDING_INTERVAL * l
    sim.run(sim_endtime)
    current_simtime = sim.getTime()
    A_count = sim.getCompCount('comp', 'A')
    B_count = sim.getCompCount('comp', 'B')
    C_count = sim.getCompCount('comp', 'C')
    D_count = sim.getCompCount('comp', 'D')
    E_count = sim.getCompCount('comp', 'E')
    F_count = sim.getCompCount('comp', 'F')
    G_count = sim.getCompCount('comp', 'G')
    H_count = sim.getCompCount('comp', 'H')
    I_count = sim.getCompCount('comp', 'I')
    J_count = sim.getCompCount('comp', 'J')

    summary_file.write(
        "%f,%i,%i,%i,%i,%i,%i,%i,%i,%i,%i\n"
        % (
            current_simtime,
            A_count,
            B_count,
            C_count,
            D_count,
            E_count,
            F_count,
            G_count,
            H_count,
            I_count,
            J_count,
        )
    )

summary_file.close()

And here is the parallel TetOpSplit version,

#  This script is provided as example for STEPS user manual.
#  License: GPL2.0
#  Contact: Dr. Weiliang Chen, w.chen@oist.jp

import os
import time

import steps
import steps.geom as stetmesh
import steps.model as smod
import steps.mpi
import steps.mpi.solver as parallel_solver
import steps.rng as srng
import steps.utilities.geom_decompose as gd
import steps.utilities.meshio as meshio

dirPath = os.path.dirname(os.path.abspath(__file__))
MESHFILE = os.path.join(dirPath, '../../meshes/parallel/10x10x100_3363tets.inp')
RESULT_DIR = os.path.join(dirPath, "parallel_result")

#  The initial molecule counts
N0A = 1000
N0B = 2000
N0C = 3000
N0D = 4000
N0E = 5000
N0F = 6000
N0G = 7000
N0H = 8000
N0I = 9000
N0J = 10000

ENDTIME = 20.0
RECORDING_INTERVAL = 1.0

########################################################################
#  Biochemical Model


def gen_model():

    mdl = smod.Model()

    # The chemical species
    A = smod.Spec('A', mdl)
    B = smod.Spec('B', mdl)
    C = smod.Spec('C', mdl)
    D = smod.Spec('D', mdl)
    E = smod.Spec('E', mdl)
    F = smod.Spec('F', mdl)
    G = smod.Spec('G', mdl)
    H = smod.Spec('H', mdl)
    I = smod.Spec('I', mdl)
    J = smod.Spec('J', mdl)

    volsys = smod.Volsys('vsys', mdl)

    R1 = smod.Reac('R1', volsys, lhs=[A, B], rhs=[C], kcst=1000.0e6)
    R2 = smod.Reac('R2', volsys, lhs=[C], rhs=[A, B], kcst=100)
    R3 = smod.Reac('R3', volsys, lhs=[C, D], rhs=[E], kcst=100e6)
    R4 = smod.Reac('R4', volsys, lhs=[E], rhs=[C, D], kcst=10)

    R5 = smod.Reac('R5', volsys, lhs=[F, G], rhs=[H], kcst=10e6)
    R6 = smod.Reac('R6', volsys, lhs=[H], rhs=[F, G], kcst=1)
    R7 = smod.Reac('R7', volsys, lhs=[H, I], rhs=[J], kcst=1e6)
    R8 = smod.Reac('R8', volsys, lhs=[J], rhs=[H, I], kcst=0.1 * 10)

    # The diffusion rules
    D1 = smod.Diff('D1', volsys, A, 100e-12)
    D2 = smod.Diff('D2', volsys, B, 90e-12)
    D3 = smod.Diff('D3', volsys, C, 80e-12)
    D4 = smod.Diff('D4', volsys, D, 70e-12)
    D5 = smod.Diff('D5', volsys, E, 60e-12)
    D6 = smod.Diff('D6', volsys, F, 50e-12)
    D7 = smod.Diff('D7', volsys, G, 40e-12)
    D8 = smod.Diff('D8', volsys, H, 30e-12)
    D9 = smod.Diff('D9', volsys, I, 20e-12)
    D10 = smod.Diff('D10', volsys, J, 10e-12)

    return mdl


########################################################################
#  Geometry
def gen_geom():
    mesh = meshio.importAbaqus(MESHFILE, 1e-6)[0]
    ntets = mesh.countTets()
    comp = stetmesh.TmComp('comp', mesh, range(ntets))
    comp.addVolsys('vsys')

    return mesh


########################################################################

m = gen_model()
g = gen_geom()

#  Geometry Partitioning

tet_hosts = gd.linearPartition(g, [1, 1, steps.mpi.nhosts])
if steps.mpi.rank == 0:
    gd.validatePartition(g, tet_hosts)
    gd.printPartitionStat(tet_hosts)

########################################################################
#  recording
if steps.mpi.rank == 0:
    try:
        os.mkdir(RESULT_DIR)
    except:
        pass

    summary_file = open(RESULT_DIR + "/result.csv", 'w', 1)
    summary_file.write("Simulation Time,A,B,C,D,E,F,G,H,I,J\n")

########################################################################

rng = srng.create('mt19937', 512)
rng.initialize(int(time.time() % 4294967295))

sim = parallel_solver.TetOpSplit(m, g, rng, parallel_solver.EF_NONE, tet_hosts)

#  Set initial conditions
sim.setCompCount('comp', 'A', N0A)
sim.setCompCount('comp', 'B', N0B)
sim.setCompCount('comp', 'C', N0C)
sim.setCompCount('comp', 'D', N0D)
sim.setCompCount('comp', 'E', N0E)
sim.setCompCount('comp', 'F', N0F)
sim.setCompCount('comp', 'G', N0G)
sim.setCompCount('comp', 'H', N0H)
sim.setCompCount('comp', 'I', N0I)
sim.setCompCount('comp', 'J', N0J)

n_tpns = int(ENDTIME / RECORDING_INTERVAL) + 1

for l in range(n_tpns):
    sim_endtime = RECORDING_INTERVAL * l
    sim.run(sim_endtime)
    current_simtime = sim.getTime()
    A_count = sim.getCompCount('comp', 'A')
    B_count = sim.getCompCount('comp', 'B')
    C_count = sim.getCompCount('comp', 'C')
    D_count = sim.getCompCount('comp', 'D')
    E_count = sim.getCompCount('comp', 'E')
    F_count = sim.getCompCount('comp', 'F')
    G_count = sim.getCompCount('comp', 'G')
    H_count = sim.getCompCount('comp', 'H')
    I_count = sim.getCompCount('comp', 'I')
    J_count = sim.getCompCount('comp', 'J')

    if steps.mpi.rank == 0:
        summary_file.write(
            "%f,%i,%i,%i,%i,%i,%i,%i,%i,%i,%i\n"
            % (
                current_simtime,
                A_count,
                B_count,
                C_count,
                D_count,
                E_count,
                F_count,
                G_count,
                H_count,
                I_count,
                J_count,
            )
        )

if steps.mpi.rank == 0:
    summary_file.close()

So what are the differences? Actually not that many. Parallel TetOpSplit is designed in the way that a serial Tetexact simulation can be easily converted to the parallel version with minimal script modifications. Here is the general procedure:

13.9.1.1. Replace the modules

# Serial Tetexact
import steps.solver as ssa_solver

# Parallel TetOpSplit
import steps.mpi
import steps.mpi.solver as parallel_solver
import steps.utilities.geom_decompose as gd

The steps.mpi module needs to be imported before the steps.mpi.solver submodule, it provides two important variables for parallel simulation, steps.mpi.nhosts provides the number of MPI processes used in the simulation, and the steps.mpi.rank provides the MPI rank of the current process.

The steps.API_1.utilities.geom_decompose module contains functions for mesh partitioning, which are often used in parallel STEPS simulations.

13.9.1.2. Partition the mesh

In the current parallel implementation, a partitioning list is required to distribute the tetrahedrons and triangles to each MPI process. the steps.API_1.utilities.geom_decompose.linearPartition() function provides a grid based partitioning solution for simple geometry:

# Partition a mesh g into n segments along the z axis,
# where n is the number of MPI processes in the simulation,
# and return the partitioning list as tet_hosts

tet_hosts = gd.linearPartition(g, [1, 1, steps.mpi.nhosts])

The three elements in the list [1, 1, steps.mpi.nhosts] represent the numbers of partitions along the x, y and z directions. the function returns a list which indicates the assigned process rank for each tetrahedron, for example, the host process for tetrahedron 2 is stored in tet_hosts[2].

For complex geometries such as a dendrite tree, grid-based partitioning may not be the best choice. In this case, other third party partitioning software such as Metis can be used. We will come back to this topic later.

If your model has patches, the steps.API_1.utilities.geom_decompose.partitionTris() function can automatically partition the patch triangles according to the tetrahedron partitioning list.

tet_hosts = gd.linearPartition(g, [1, 1, steps.mpi.nhosts])
tri_hosts = gd.partitionTris(g, tet_hosts, YOUR_TRI_ID_LIST)

You can validate and print out the stats of your partitioning like this

if steps.mpi.rank == 0:
    gd.validatePartition(g, tet_hosts)
    gd.printPartitionStat(tet_hosts)

The if line is needed because we only want process 0 to print out the text.

13.9.1.3. Create files for recording

It is often necessary to record data from the simulation, in a serial Tetexact simulation, the data files can be created easily like this

# create a summary file "result.csv" in the "RESULT_DIR" directory

try: os.mkdir(RESULT_DIR)
except: pass

summary_file = open(RESULT_DIR + "/result.csv", 'w', 0)
summary_file.write("Simulation Time,A,B,C,D,E,F,G,H,I,J\n")

However, in a parallel TetOpSplit simulation, you need to consider which process is responsible for data recording. There are two commonly used approaches, firstly, assign one process (such as process 0) specifically for recording

if steps.mpi.rank == 0:
    try: os.mkdir(RESULT_DIR)
    except: pass

    summary_file = open(RESULT_DIR + "/result.csv", 'w', 0)
    summary_file.write("Simulation Time,A,B,C,D,E,F,G,H,I,J\n")

or secondly, each process record a copy of the data

if steps.mpi.rank == 0:
    try: os.mkdir(RESULT_DIR)
    except: pass

summary_file = open(RESULT_DIR + "/result_proc%i.csv" % (steps.mpi.rank), 'w', 0)
summary_file.write("Simulation Time,A,B,C,D,E,F,G,H,I,J\n")

Which approach you use depends on what data you want to record, functions like steps.API_1.mpi.solver.TetOpSplit.getCompCount() needs to be called in every process and returns the same result to each process when called; on the other hand, steps.API_1.mpi.solver.TetOpSplit.getIdleTime() returns different result for each process, in which case the second recording method is necessary.

13.9.1.4. Create solver and run the simulation

We now create a TetOpSplit solver to replace the Tetexact solver

# Serial Tetexact
sim = ssa_solver.Tetexact(m, g, rng)

# Parallel TetOpSplit
sim = parallel_solver.TetOpSplit(m, g, rng, parallel_solver.EF_NONE, tet_hosts)

parallel_solver.EF_NONE tells the solver that no parallel EField solver is needed for the simulation, we will talk about the parallel EField solvers later. tet_hosts is the tetrahedron partitioning list we generated above. If your model has patches, you also need to fill in the triangle partitioning info.

sim = parallel_solver.TetOpSplit(m, g, rng, parallel_solver.EF_NONE, tet_hosts, tri_hosts)

You can control the simulation run pretty much the same as the serial solver, just need to remember that if you use a specific process for data recording, you need to ask the assigned process to write the data alone.

if steps.mpi.rank == 0:
    summary_file.write("%f,%i,%i,%i,%i,%i,%i,%i,%i,%i,%i\n" % \
    (current_simtime, A_count, B_count, C_count, D_count, E_count, \
    F_count, G_count, H_count, I_count, J_count))

Also note that steps.API_1.mpi.solver.TetOpSplit.getCompCount() is a global collective function that needs to be called in every process at the same time (including most functions inherited from Tetexact), so you cannot do the following

# this is not correct
if steps.mpi.rank == 0:
    summary_file.write("%i" % sim.getCompCount('comp', 'A'))

At the end of your simulation, remember to close the data file and we are done.

if steps.mpi.rank == 0:
    summary_file.close()

13.9.1.5. Simulation execution

Youc can run a parallel TetOpSplit simulation by calling ‘mpirun’ or similar executable provided by your MPI distribution.

mpirun -n NPROCS python my_parallel_sim.py

NPROCS is the number of MPI processes used in your simulation.

13.9.2. Complex Mesh Partitioning

The grid-based partitioning approach may not be suitable for complex geometries, such as a dendritic tree, in this case, we suggest use third party partitioning tools such as Metis. The steps.API_1.utilities.metis_support module provides supporting functions for data exchange between STEPS and Metis. To partition a STEPS Tetmesh using Metis, we need to first convert the tetrahedron connectivity information in the mesh to Metis format,

import steps.utilities.geom_decompose as gd
import steps.utilities.meshio as meshio
import steps.utilities.metis_support as metis

MESH_FILE = "mymesh.inp"
mesh = meshio.importAbaqus(MESH_FILE, 1e-6)[0]

# save the connectivity to mymesh.metis
metis.tetmesh2metis(mesh, 'mymesh.metis')

then call Metis either from a bash terminal,

mpmetis -ncommon=3 -minconn -niter=1000 mymesh.metis 10

or from python

call(['mpmetis', '-ncommon=3', '-minconn', '-niter=1000', 'mymesh.metis', '10'])

Metis will partition the mesh into 10 segments and store the partition information to “mymesh.metis.epart.10”. Details of Metis parameters can be found in Metis User Mamnual. After the partitioning, you can read the partition information from the file using

tet_hosts = metis.readPartition('mymesh.metis.epart.10')

and use it to construct your TetOpSplit solver.

If you have PyQtGraph and PyOpenGL installed, you can visualize the partitions of the mesh using

import steps.visual
import pyqtgraph as pg
app = pg.mkQApp()

w = steps.visual.TetPartitionDisplay(mesh, tet_hosts, w = 1200, h = 800)
w = steps.visual.TriPartitionDisplay(mesh, tri_hosts, w = 1200, h = 800)
app.exec_()

Figure below shows the difference between partitioning using grid-based STEPS toolkit and Metis, on a dendritic tree morphology.

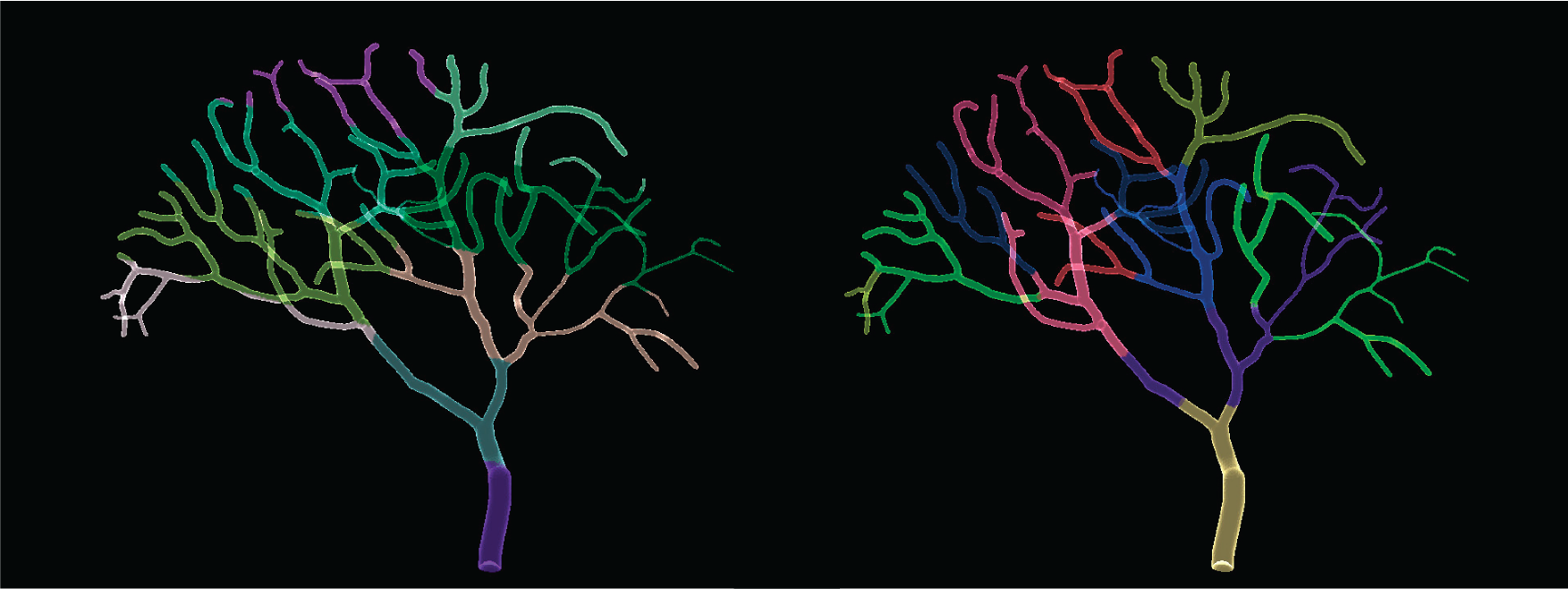
Visual comparision of grid-based (left) partitioning and partitioning using Metis (right). Each color represents a mesh partition to be assigned to a MPI process.

13.9.3. Parallel EField Simulation

The parallel TetOpSplit solver in STEPS 3.0.0 includes several prototypes for combined simulations with both reaction-diffusion and EField. The prototypes can be switched by changing the calcMembPot parameter in the TetOpSplit constructor. Here are the possible options:

• steps.mpi.solver.EF_NONE

  No EField solver is needed.

• steps.mpi.solver.EF_DEFAULT

  Run serial EField simulation (Tetexact version) on process 0.

• steps.mpi.solver.EF_DV_BDSYS

  Use parallel SuperLU EField solver.

• steps.mpi.solver.EF_DV_PETSC

  Use parallel PETSc EField solver.

The default value is EF_NONE, i.e. no EField is simulated. For scale EFIeld simulation we recommand the EF_DV_BDSYS solver, for large scale EField simulation we recommand the EF_DV_PETSC solver.

Here is an example of the Hodgkin-Huxley Action Potential propagation simulation (see Simulating Membrane Potential) using parallel TetOpSplit with SuperLU EField solver.

#  This script is provided as example for STEPS user manual.
#  License: GPL2.0
#  Parallel modification for user manual
#  Contact: Dr. Weiliang Chen, w.chen@oist.jp

#  Original
#  Example: Hodgkin-Huxley Action Potential propagation model
#  Author Iain Hepburn
#  http://steps.sourceforge.net/manual/memb_pot.html

# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #

# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #
# # # # # # # # # # # # # # # # # # # IMPORTS # # # # # # # # # # # # # # # # # #
# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #

from __future__ import print_function

import math
import os
import time
from random import *

import numpy

import steps.geom as sgeom
import steps.model as smodel
import steps.mpi
import steps.mpi.solver as mpi_solver
import steps.rng as srng
import steps.utilities.geom_decompose as gd
import steps.utilities.meshio as meshio
from pylab import *

# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #
# # # # # # # # # # # # # # # # # # PARAMETERS  # # # # # # # # # # # # # # # # #
# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #

# # # # # # # # # # # # # # # # # # CHANNELS  # # # # # # # # # # # # # # # # # #

#  Potassium conductance = 0.036 S/cm2
#  Sodium conductance = 0.120 S/cm2

#  Potassium single-channel conductance
K_G = 20.0e-12  # Siemens

#  Potassium channel density
K_ro = 18.0e12  # per square meter

#  Potassium reversal potential
K_rev = -77e-3  # volts

#  Sodium single-channel conductance
Na_G = 20.0e-12  # Siemens

#  Sodium channel density
Na_ro = 60.0e12  # per square meter

#  Sodium reversal potential
Na_rev = 50e-3  # volts

#  Leak single-channel conductance
L_G = 0.3e-12  # Siemens

#  Leak density
L_ro = 10.0e12  # per square meter

#  Leak reveral potential
leak_rev = -54.4e-3  # volts


#  A table of potassium channel population factors:
#  n0, n1, n2, n3, n4
K_facs = [0.21768, 0.40513, 0.28093, 0.08647, 0.00979]

#  A table of sodium channel population factors
#  m0h0, m1h0, m2h0, m3h0, m0h1, m1h1, m2h1, m3h1:
Na_facs = [0.34412, 0.05733, 0.00327, 6.0e-05, 0.50558, 0.08504, 0.00449, 0.00010]

# # # # # # # # # # # # # # # # # # MESH  # # # # # # # # # # # # # # # # # # # #

dirPath = os.path.dirname(os.path.abspath(__file__))
meshPath = os.path.join(dirPath, '../../meshes/parallel/axon_cube_L1000um_D443nm_equiv0.5_19087tets.inp')

# # # # # # # # # # # # # # # SIMULATION CONTROLS # # # # # # # # # # # # # # # #

#  Temperature for gating kinetics
celsius = 20.0

#  Current injection
Iclamp = 50.0e-12  # amps

#  Voltage range for gating kinetics in Volts
Vrange = [-100.0e-3, 50e-3, 1e-4]

#  The number of simulation time-points
N_timepoints = 41

#  The simulation dt
DT_sim = 1.0e-4  # seconds

# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #
# # # # # # # # # # # # # # # BIOCHEMICAL MODEL # # # # # # # # # # # # # # # # #
# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #

mdl = smodel.Model()
ssys = smodel.Surfsys('ssys', mdl)

#  Potassium channel
K = smodel.Chan('K', mdl)
K_n0 = smodel.ChanState('K_n0', mdl, K)
K_n1 = smodel.ChanState('K_n1', mdl, K)
K_n2 = smodel.ChanState('K_n2', mdl, K)
K_n3 = smodel.ChanState('K_n3', mdl, K)
K_n4 = smodel.ChanState('K_n4', mdl, K)

#  Sodium channel
Na = smodel.Chan('Na', mdl)
Na_m0h0 = smodel.ChanState('Na_m0h0', mdl, Na)
Na_m1h0 = smodel.ChanState('Na_m1h0', mdl, Na)
Na_m2h0 = smodel.ChanState('Na_m2h0', mdl, Na)
Na_m3h0 = smodel.ChanState('Na_m3h0', mdl, Na)
Na_m0h1 = smodel.ChanState('Na_m0h1', mdl, Na)
Na_m1h1 = smodel.ChanState('Na_m1h1', mdl, Na)
Na_m2h1 = smodel.ChanState('Na_m2h1', mdl, Na)
Na_m3h1 = smodel.ChanState('Na_m3h1', mdl, Na)

#  Leak channel
L = smodel.Chan('L', mdl)
Leak = smodel.ChanState('Leak', mdl, L)

# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #

#  Hodgkin-Huxley gating kinetics

#  Temperature dependence
thi = math.pow(3.0, ((celsius - 6.3) / 10.0))

_a_n = lambda mV: thi * (
    (0.01 * (10 - (mV + 65.0)) / (math.exp((10 - (mV + 65.0)) / 10.0) - 1))
)

_b_n = lambda mV: thi * ((0.125 * math.exp(-(mV + 65.0) / 80.0)))

_a_m = lambda mV: thi * (
    (0.1 * (25 - (mV + 65.0)) / (math.exp((25 - (mV + 65.0)) / 10.0) - 1))
)

_b_m = lambda mV: thi * ((4.0 * math.exp(-(mV + 65.0) / 18.0)))


_a_h = lambda mV: thi * ((0.07 * math.exp(-(mV + 65.0) / 20.0)))

_b_h = lambda mV: thi * ((1.0 / (math.exp((30 - (mV + 65.0)) / 10.0) + 1)))


# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #

Kn0n1 = smodel.VDepSReac(
    'Kn0n1',
    ssys,
    slhs=[K_n0],
    srhs=[K_n1],
    k=lambda V: 1.0e3 * 4.0 * _a_n(V * 1.0e3),
    vrange=Vrange,
)
Kn1n2 = smodel.VDepSReac(
    'Kn1n2',
    ssys,
    slhs=[K_n1],
    srhs=[K_n2],
    k=lambda V: 1.0e3 * 3.0 * _a_n(V * 1.0e3),
    vrange=Vrange,
)
Kn2n3 = smodel.VDepSReac(
    'Kn2n3',
    ssys,
    slhs=[K_n2],
    srhs=[K_n3],
    k=lambda V: 1.0e3 * 2.0 * _a_n(V * 1.0e3),
    vrange=Vrange,
)
Kn3n4 = smodel.VDepSReac(
    'Kn3n4',
    ssys,
    slhs=[K_n3],
    srhs=[K_n4],
    k=lambda V: 1.0e3 * 1.0 * _a_n(V * 1.0e3),
    vrange=Vrange,
)

Kn4n3 = smodel.VDepSReac(
    'Kn4n3',
    ssys,
    slhs=[K_n4],
    srhs=[K_n3],
    k=lambda V: 1.0e3 * 4.0 * _b_n(V * 1.0e3),
    vrange=Vrange,
)
Kn3n2 = smodel.VDepSReac(
    'Kn3n2',
    ssys,
    slhs=[K_n3],
    srhs=[K_n2],
    k=lambda V: 1.0e3 * 3.0 * _b_n(V * 1.0e3),
    vrange=Vrange,
)
Kn2n1 = smodel.VDepSReac(
    'Kn2n1',
    ssys,
    slhs=[K_n2],
    srhs=[K_n1],
    k=lambda V: 1.0e3 * 2.0 * _b_n(V * 1.0e3),
    vrange=Vrange,
)
Kn1n0 = smodel.VDepSReac(
    'Kn1n0',
    ssys,
    slhs=[K_n1],
    srhs=[K_n0],
    k=lambda V: 1.0e3 * 1.0 * _b_n(V * 1.0e3),
    vrange=Vrange,
)

# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #

Na_m0h1_m1h1 = smodel.VDepSReac(
    'Na_m0h1_m1h1',
    ssys,
    slhs=[Na_m0h1],
    srhs=[Na_m1h1],
    k=lambda V: 1.0e3 * 3.0 * _a_m(V * 1.0e3),
    vrange=Vrange,
)
Na_m1h1_m2h1 = smodel.VDepSReac(
    'Na_m1h1_m2h1',
    ssys,
    slhs=[Na_m1h1],
    srhs=[Na_m2h1],
    k=lambda V: 1.0e3 * 2.0 * _a_m(V * 1.0e3),
    vrange=Vrange,
)
Na_m2h1_m3h1 = smodel.VDepSReac(
    'Na_m2h1_m3h1',
    ssys,
    slhs=[Na_m2h1],
    srhs=[Na_m3h1],
    k=lambda V: 1.0e3 * 1.0 * _a_m(V * 1.0e3),
    vrange=Vrange,
)

Na_m3h1_m2h1 = smodel.VDepSReac(
    'Na_m3h1_m2h1',
    ssys,
    slhs=[Na_m3h1],
    srhs=[Na_m2h1],
    k=lambda V: 1.0e3 * 3.0 * _b_m(V * 1.0e3),
    vrange=Vrange,
)
Na_m2h1_m1h1 = smodel.VDepSReac(
    'Na_m2h1_m1h1',
    ssys,
    slhs=[Na_m2h1],
    srhs=[Na_m1h1],
    k=lambda V: 1.0e3 * 2.0 * _b_m(V * 1.0e3),
    vrange=Vrange,
)
Na_m1h1_m0h1 = smodel.VDepSReac(
    'Na_m1h1_m0h1',
    ssys,
    slhs=[Na_m1h1],
    srhs=[Na_m0h1],
    k=lambda V: 1.0e3 * 1.0 * _b_m(V * 1.0e3),
    vrange=Vrange,
)

Na_m0h0_m1h0 = smodel.VDepSReac(
    'Na_m0h0_m1h0',
    ssys,
    slhs=[Na_m0h0],
    srhs=[Na_m1h0],
    k=lambda V: 1.0e3 * 3.0 * _a_m(V * 1.0e3),
    vrange=Vrange,
)
Na_m1h0_m2h0 = smodel.VDepSReac(
    'Na_m1h0_m2h0',
    ssys,
    slhs=[Na_m1h0],
    srhs=[Na_m2h0],
    k=lambda V: 1.0e3 * 2.0 * _a_m(V * 1.0e3),
    vrange=Vrange,
)
Na_m2h0_m3h0 = smodel.VDepSReac(
    'Na_m2h0_m3h0',
    ssys,
    slhs=[Na_m2h0],
    srhs=[Na_m3h0],
    k=lambda V: 1.0e3 * 1.0 * _a_m(V * 1.0e3),
    vrange=Vrange,
)

Na_m3h0_m2h0 = smodel.VDepSReac(
    'Na_m3h0_m2h0',
    ssys,
    slhs=[Na_m3h0],
    srhs=[Na_m2h0],
    k=lambda V: 1.0e3 * 3.0 * _b_m(V * 1.0e3),
    vrange=Vrange,
)
Na_m2h0_m1h0 = smodel.VDepSReac(
    'Na_m2h0_m1h0',
    ssys,
    slhs=[Na_m2h0],
    srhs=[Na_m1h0],
    k=lambda V: 1.0e3 * 2.0 * _b_m(V * 1.0e3),
    vrange=Vrange,
)
Na_m1h0_m0h0 = smodel.VDepSReac(
    'Na_m1h0_m0h0',
    ssys,
    slhs=[Na_m1h0],
    srhs=[Na_m0h0],
    k=lambda V: 1.0e3 * 1.0 * _b_m(V * 1.0e3),
    vrange=Vrange,
)

Na_m0h0_m0h1 = smodel.VDepSReac(
    'Na_m0h0_m0h1',
    ssys,
    slhs=[Na_m0h0],
    srhs=[Na_m0h1],
    k=lambda V: 1.0e3 * _a_h(V * 1.0e3),
    vrange=Vrange,
)
Na_m1h0_m1h1 = smodel.VDepSReac(
    'Na_m1h0_m1h1',
    ssys,
    slhs=[Na_m1h0],
    srhs=[Na_m1h1],
    k=lambda V: 1.0e3 * _a_h(V * 1.0e3),
    vrange=Vrange,
)
Na_m2h0_m2h1 = smodel.VDepSReac(
    'Na_m2h0_m2h1',
    ssys,
    slhs=[Na_m2h0],
    srhs=[Na_m2h1],
    k=lambda V: 1.0e3 * _a_h(V * 1.0e3),
    vrange=Vrange,
)
Na_m3h0_m3h1 = smodel.VDepSReac(
    'Na_m3h0_m3h1',
    ssys,
    slhs=[Na_m3h0],
    srhs=[Na_m3h1],
    k=lambda V: 1.0e3 * _a_h(V * 1.0e3),
    vrange=Vrange,
)

Na_m0h1_m0h0 = smodel.VDepSReac(
    'Na_m0h1_m0h0',
    ssys,
    slhs=[Na_m0h1],
    srhs=[Na_m0h0],
    k=lambda V: 1.0e3 * _b_h(V * 1.0e3),
    vrange=Vrange,
)
Na_m1h1_m1h0 = smodel.VDepSReac(
    'Na_m1h1_m1h0',
    ssys,
    slhs=[Na_m1h1],
    srhs=[Na_m1h0],
    k=lambda V: 1.0e3 * _b_h(V * 1.0e3),
    vrange=Vrange,
)
Na_m2h1_m2h0 = smodel.VDepSReac(
    'Na_m2h1_m2h0',
    ssys,
    slhs=[Na_m2h1],
    srhs=[Na_m2h0],
    k=lambda V: 1.0e3 * _b_h(V * 1.0e3),
    vrange=Vrange,
)
Na_m3h1_m3h0 = smodel.VDepSReac(
    'Na_m3h1_m3h0',
    ssys,
    slhs=[Na_m3h1],
    srhs=[Na_m3h0],
    k=lambda V: 1.0e3 * _b_h(V * 1.0e3),
    vrange=Vrange,
)

# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #

#  Create ohmic current objects

OC_K = smodel.OhmicCurr('OC_K', ssys, chanstate=K_n4, g=K_G, erev=K_rev)
OC_Na = smodel.OhmicCurr('OC_Na', ssys, chanstate=Na_m3h1, g=Na_G, erev=Na_rev)
OC_L = smodel.OhmicCurr('OC_L', ssys, chanstate=Leak, g=L_G, erev=leak_rev)

# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #
# # # # # # # # # # # # # # # TETRAHEDRAL MESH  # # # # # # # # # # # # # # # # #
# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #

mesh = meshio.importAbaqus(meshPath, 1e-6)[0]
tet_hosts = gd.binTetsByAxis(mesh, steps.mpi.nhosts)
tri_hosts = gd.partitionTris(mesh, tet_hosts, mesh.getSurfTris())

# # # # # # # # # # # # # # # MESH MANIPULATION # # # # # # # # # # # # # # # # #

#  Find the vertices for the current clamp and store in a list
injverts = []
for i in range(mesh.nverts):
    if mesh.getVertex(i)[2] < (mesh.getBoundMin()[2] + 0.1e-6):
        injverts.append(i)
if steps.mpi.rank == 0:
    print("Found ", injverts.__len__(), "I_inject vertices")

facetris = []
for i in range(mesh.ntris):
    tri = mesh.getTri(i)
    if (tri[0] in injverts) and (tri[1] in injverts) and (tri[2] in injverts):
        facetris.append(i)
if steps.mpi.rank == 0:
    print("Found ", facetris.__len__(), "triangles on bottom face")

memb_tris = list(mesh.getSurfTris())

#  Remove triangles on bottom face from membrane triangles
for t in facetris:
    memb_tris.remove(t)

#  The points along (z) axis at which to record potential
pot_pos = numpy.arange(mesh.getBoundMin()[2], mesh.getBoundMax()[2], 10e-6)
pot_n = len(pot_pos)

pot_tet = numpy.zeros(pot_n, dtype='uint')

i = 0
for p in pot_pos:
    # Axis is aligned with z-axis
    pot_tet[i] = mesh.findTetByPoint([0.0, 0.0, pot_pos[i]])
    i = i + 1

# # # # # # # # # # # # # # # GEOMETRY OBJECTS  # # # # # # # # # # # # # # # # #

#  Create cytosol compartment
cyto = sgeom.TmComp('cyto', mesh, range(mesh.ntets))

#  Create the patch and associate with surface system 'ssys'
patch = sgeom.TmPatch('patch', mesh, memb_tris, cyto)
patch.addSurfsys('ssys')

#  Create the membrane across which the potential will be solved
membrane = sgeom.Memb('membrane', mesh, [patch], opt_method=1)

# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #

#  Create the random number generator
r = srng.create('mt19937', 512)
r.initialize(int(time.time() % 10000))

# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #
# # # # # # # # # # # # # # # # # SIMULATION  # # # # # # # # # # # # # # # # # #
# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #

#  Create solver object using SuperLU EField solver
sim = mpi_solver.TetOpSplit(mdl, mesh, r, mpi_solver.EF_DV_BDSYS, tet_hosts, tri_hosts)

# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #

#  Inject channels

surfarea = sim.getPatchArea('patch')

sim.setPatchCount('patch', 'Na_m0h0', Na_ro * surfarea * Na_facs[0])
sim.setPatchCount('patch', 'Na_m1h0', Na_ro * surfarea * Na_facs[1])
sim.setPatchCount('patch', 'Na_m2h0', Na_ro * surfarea * Na_facs[2])
sim.setPatchCount('patch', 'Na_m3h0', Na_ro * surfarea * Na_facs[3])
sim.setPatchCount('patch', 'Na_m0h1', Na_ro * surfarea * Na_facs[4])
sim.setPatchCount('patch', 'Na_m1h1', Na_ro * surfarea * Na_facs[5])
sim.setPatchCount('patch', 'Na_m2h1', Na_ro * surfarea * Na_facs[6])
sim.setPatchCount('patch', 'Na_m3h1', Na_ro * surfarea * Na_facs[7])

sim.setPatchCount('patch', 'K_n0', K_ro * surfarea * K_facs[0])
sim.setPatchCount('patch', 'K_n1', K_ro * surfarea * K_facs[1])
sim.setPatchCount('patch', 'K_n2', K_ro * surfarea * K_facs[2])
sim.setPatchCount('patch', 'K_n3', K_ro * surfarea * K_facs[3])
sim.setPatchCount('patch', 'K_n4', K_ro * surfarea * K_facs[4])

sim.setPatchCount('patch', 'Leak', L_ro * surfarea)

# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #

#  Set some simulation variables:

#  Set dt for membrane potential calculation to 0.01ms
sim.setEfieldDT(1.0e-5)

#  Initialize potential to -65mV
sim.setMembPotential('membrane', -65e-3)

#  Set capacitance of the membrane to 1 uF/cm^2 = 0.01 F/m^2
sim.setMembCapac('membrane', 1.0e-2)

#  Set resistivity of the conduction volume to 100 ohm.cm = 1 ohm.meter
sim.setMembVolRes('membrane', 1.0)

# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #
#  Set the current clamp
niverts = injverts.__len__()
for t in injverts:
    sim.setVertIClamp(t, Iclamp / niverts)

# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #

#  Create result structures
if steps.mpi.rank == 0:
    res = numpy.zeros((N_timepoints, pot_n))

# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #

#  Run the simulation
for l in range(N_timepoints):
    if steps.mpi.rank == 0:
        print("Tpnt: ", l, "/", N_timepoints)

    sim.run(DT_sim * l)

    if steps.mpi.rank == 0:
        for p in range(pot_n):
            res[l, p] = sim.getTetV(int(pot_tet[p])) * 1.0e3

# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #

if steps.mpi.rank == 0:
    results = (res, pot_pos)
    tpnt = arange(0.0, N_timepoints * DT_sim, DT_sim)

    for tidx in (0, 10, 20, 30, 40):
        plot(
            results[1] * 1e6,
            results[0][tidx],
            label=str(1e3 * tidx * DT_sim) + 'ms',
            linewidth=3,
        )
    legend(numpoints=1)
    xlim(0, 1000)
    ylim(-80, 40)
    xlabel('Z-axis (um)')
    ylabel('Membrane potential (mV)')
    show()

# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #