9. Parallel simulations

Topics: Parallel solvers, Mesh partitioning.

Parallel simulations are run with the 'TetOpSplit' solver, which supports parallel stochastic spatial reaction-difusion-EField simulations. Note however that this solver does not support dynamic load balancing.

For more details about the accuracy and performace of the parallel TetOpSplit solver, please check the following papers:

Hepburn, I., Chen, W., and De Schutter, E. (2016). Accurate reaction-diffusion operator splitting on tetrahedral meshes for parallel stochastic molecular simulations. J. Chem. Phys. 145, 054118–22. doi:10.1063/1.4960034.

Chen W and De Schutter E (2017). Parallel STEPS: Large Scale Stochastic Spatial Reaction-Diffusion Simulation with High Performance Computers. Front. Neuroinform. 11:13. doi: 10.3389/fninf.2017.00013.

9.1. Converting serial simulations to parallel

We will focus here on models involving tetrahedral meshes. So far, in these cases, we created the simulation object with the 'Tetexact' serial solver. In order to parallelize these simulations, we need to decide on a way to partition the tetrahedral mesh so that each part is run in a separate process. The first thing that we need to do is thus to declare this partition.

9.1.1. Partitioning the mesh

9.1.1.1. Linear mesh partition

Mesh partitions are usually created by using one of the available dedicated functions. The simplest one consists in partitioning the mesh along a 3D grid:

import steps.interface

from steps.geom import *

# ...

part = LinearMeshPartition(mesh, xbins, ybins, zbins)

In this example, we removed the mesh declaration code in order to focus on the partitioning. The LinearMeshPartition function takes the mesh as first parameter and then 3 integers that represent the number of bins along the x, y, and z axis respectively. Assuming the mesh is much longer on the x-axis than on the two others, we could parition the mesh in 10 bins along the x-axis only with LinearMeshPartition(mesh, 10, 1, 1).

This partition function first paritions tetrahedrons according to their position. If patches are present in the model, their triangles will automatically be partitioned according to the tetrahedron partitions.

9.1.1.2. Complex mesh partition

The grid-based partitioning approach may not be suitable for complex geometries, such as a dendritic tree, in this case, we suggest using third party partitioning tools such as Metis. To partition a STEPS TetMesh using Metis, we first need to convert the tetrahedron connectivity information in the mesh to Metis format:

mesh.ConvertToMetis('/path/to/file/mymesh.metis')

We then call Metis from a bash terminal:

mpmetis -ncommon=3 -minconn -niter=1000 mymesh.metis 10

Metis will partition the mesh into 10 segments and store the partition information to “mymesh.metis.epart.10”. Details of Metis parameters can be found in the Metis user manual. After the partitioning, you can read the partition information from the file with:

part = MetisPartition('/path/to/file/mymesh.metis.epart.10')

9.1.1.3. Manual mesh partition

The LinearMeshPartition and MetisPartition functions both return a MeshPartition object. It is possible to directly construct a MeshPartition by explicitely specifying which tetrahedrons and triangles should be attributed to which partition:

def getTetPartition(tet):
    # ...

def getTriPartition(tri):
    # ...

tet_hosts = [getTetPartition(tet) for tet in mesh.tets]

tri_hosts = {}
for patch in mesh.ALL(Patch):
    for tri in patch.tris:
        tri_hosts[tri.idx] = getTriPartition(tri)

part = MeshPartition(mesh, tet_hosts, tri_hosts)

In this example, we assume that we have two functions : getTetPartition that takes a tetrahedron as a parameter and returns an integer partition index ; and getTriPartition that takes a triangle as a parameter and returns an integer partition index. We then create the tet_hosts list that will associate each tetrahedron to an integer partition index. All tetrahedrons need to be partitioned so the length of the list is equal to the number of tetrahedrons in the mesh. Triangles only need to be partitioned if they are part of a Patch. We thus loop over all Patch objects in the mesh and build the tri_hosts dictionary that associates a triangle index to an integer partition index.

Finally, we create the partition object by simply passing the mesh along with tet_hosts and tri_hosts to the MeshPartition constructor. More details are available in the documentation.

9.1.1.4. Visualizing partitions

If PyQtGraph and PyOpenGL are installed, partitions can be visualized using the visual module (see corresponding guide):

from steps.visual import *

# ...

sc = SimControl()
with sc:
    PartitionDisplay(part)
sc.run()

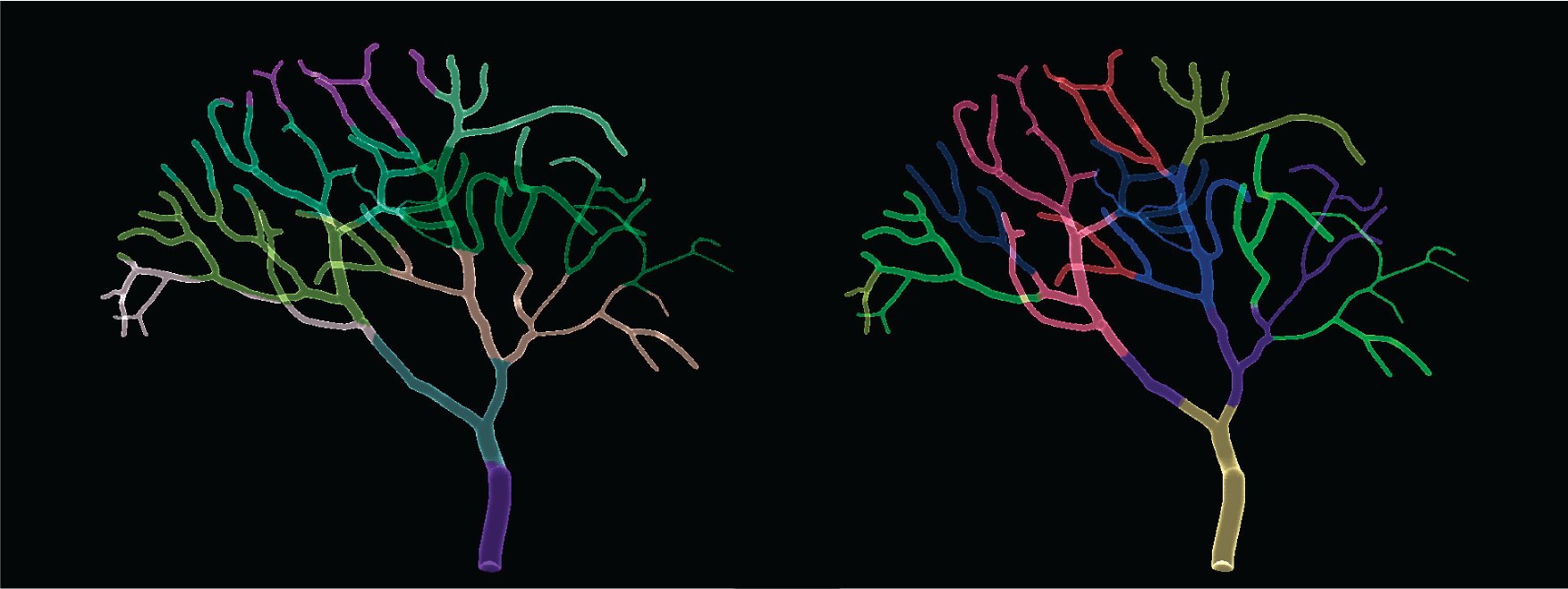
This will display the tetrahedron partitions, PartitionDisplay(part, 'tri') will instead display the triangles partitions. The image below is a comparison between a LinearMeshPartition (left) and a MetisPartition (right), each color represents a partition to be assigned to an MPI process.

9.1.2. Using parallel solvers

After having partitioned the mesh, we only need to change the solver from 'Tetexact' to 'TetOpSplit':

# ...
sim = Simulation('TetOpSplit', model, mesh, rng, True, part)
# ...

In this example, we took the Simulation construction from the previous chapter, changed 'Tetexact' to 'TetOpSplit' and added the mesh partition part as 6th parameter. These changes alone (create a mesh partition, use the 'TetOpSplit' solver) are enough to convert a script from serial to parallel.

If, during the execution, we need to manually save data or print messages to screen, this should only be done in one of the MPI processes. We can check in which MPI process we are by using the MPI class fomr the sim module:

from steps.sim import *

#...

if MPI.rank == 0:
    print(...)

MPI.rank returns the rank of the current MPI process. We can get the total number of processes with MPI.nhosts.

9.1.2.1. Parallel EField simulations

The 'TetOpSplit' solver can compute membrane potentials in different ways. As we saw in the previous chapter, membrane potential computation can be turned on by passing True as 5th parameter of the Simulation constructor. It is however also, when using 'TetOpSplit', to pass any of the following values:

• MPI.EF_NONE (equivalent to False): No EField solver is needed;

• MPI.EF_DEFAULT (equvalent to True): Run serial EField simulation (Tetexact version) on process 0;

• MPI.EF_DV_BDSYS: Use parallel SuperLU EField solver;

• MPI.EF_DV_PETSC: Use parallel PETSc EField solver.

For small scale EFIeld simulation we recommand the MPI.EF_DV_BDSYS parameter, for large scale EField simulation we recommand the MPI.EF_DV_PETSC parameter.

9.1.3. Running parallel simulations

You can run a parallel 'TetOpSplit' simulation by calling ‘mpirun’ or similar executable provided by your MPI distribution.

mpirun -n NPROCS python3 STEPS_Tutorial_MPI.py

NPROCS is the number of MPI processes that should be used.

9.1.4. Example

We now turn to converting the previous chapter simulation from serial to parallel. We use the 'TetOpSplit' solver with the SuperLU Efield solver:

The corresponding python scripts: STEPS_Tutorial_MPI.py and STEPS_Tutorial_MPI_plot.py

# Example: Parallel simulations
# http://steps.sourceforge.net/manual/API_2/STEPS_Tutorial_MPI.html

# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #

import steps.interface

from steps.model import *
from steps.geom import *
from steps.sim import *
from steps.saving import *
from steps.rng import *

import numpy as np
import math

# Potassium conductance = 0.036 S/cm2

# Potassium single-channel conductance
K_G = 20.0e-12 # Siemens

# Potassium channel density
K_ro = 18.0e12 # per square meter

# Potassium reversal potential
K_rev = -77e-3 # volts

# Sodium conductance = 0.120 S/cm2

# Sodium single-channel conductance
Na_G = 20.0e-12 # Siemens

# Sodium channel density
Na_ro = 60.0e12 # per square meter

# Sodium reversal potential
Na_rev = 50e-3 # volts

# Leak single-channel conductance
L_G = 0.3e-12 # Siemens

# Leak density
L_ro = 10.0e12 # per square meter

# Leak reveral potential
leak_rev = -54.4e-3 # volts

# A table of potassium channel population factors:
# n0, n1, n2, n3, n4
K_facs = [ 0.21768, 0.40513, 0.28093, 0.08647, 0.00979 ]

# A table of sodium channel population factors
# m0h0, m1h0, m2h0, m3h0, m0h1, m1h1, m2h1, m3h1:
Na_facs = [[0.34412, 0.05733, 0.00327, 6.0e-05],
           [0.50558, 0.08504, 0.00449, 0.00010]]

# Temperature for gating kinetics
celsius = 20.0

# Current injection
Iclamp = 50.0e-12 # amps

# Voltage range for gating kinetics in Volts
Vrange = [-100.0e-3, 50e-3, 1e-4]

def HHRateFunction(A, B, C, D, F, H, V):
    num = A + B * V
    denom = C + H * math.exp((V + D) / F)
    if num == denom == 0:
        return F * B / (H * math.exp((V + D) / F))
    else:
        return num / denom

# The simulation dt
DT_sim = 1.0e-4 # seconds

# The time until which the simulation should be run
ENDT = 4.0e-3

#########################
# Model setup
#########################

model = Model()

r = ReactionManager()

with model:
    ssys = SurfaceSystem.Create()

    #  Potassium channel
    Ko, Kc = SubUnitState.Create()
    KSU = SubUnit.Create([Ko, Kc])
    VGKC = Channel.Create([KSU]*4)

    # Sodium channel
    Na_mo, Na_mc, Na_hi, Na_ha = SubUnitState.Create()
    NamSU, NahSU = SubUnit.Create(
        [Na_mo, Na_mc],
        [Na_hi, Na_ha]
    )
    VGNaC = Channel.Create([NamSU, NamSU, NamSU, NahSU])

    # Leak channel
    lsus = SubUnitState.Create()
    Leak = Channel.Create([lsus])

    thi = math.pow(3.0, ((celsius-6.3)/10.0))

    _a_n = VDepRate(
        lambda V: thi * 1e3 * HHRateFunction(-0.55, -0.01, -1, 55, -10, 1, V*1e3),
        vrange=Vrange
    )
    _b_n = VDepRate(
        lambda V: thi * 1e3 * HHRateFunction(1, 0, 0, 65, 80, 8, V*1e3),
        vrange=Vrange
    )

    _a_m = VDepRate(
        lambda V: thi * 1e3 * HHRateFunction(-4, -0.1, -1, 40, -10, 1, V*1e3),
        vrange=Vrange
    )
    _b_m = VDepRate(
        lambda V: thi * 1e3 * HHRateFunction(1, 0, 0, 65, 18, 0.25, V*1e3),
        vrange=Vrange
    )

    _a_h = VDepRate(
        lambda V: thi * 1e3 * HHRateFunction(1, 0, 0, 65, 20, 1 / 0.07, V*1e3),
        vrange=Vrange
    )
    _b_h = VDepRate(
        lambda V: thi * 1e3 * HHRateFunction(1, 0, 1, 35, -10, 1, V*1e3),
        vrange=Vrange
    )

    with ssys:
        with VGKC[...]:
            Kc.s <r[1]> Ko.s
            r[1].K = _a_n, _b_n

        with VGNaC[...]:
            Na_hi.s <r[1]> Na_ha.s
            r[1].K = _a_h, _b_h

            Na_mc.s <r[1]> Na_mo.s
            r[1].K = _a_m, _b_m

        VGKC_I = OhmicCurr.Create(VGKC[Ko, Ko, Ko, Ko], K_G, K_rev)
        VGNaC_I = OhmicCurr.Create(VGNaC[Na_mo, Na_mo, Na_mo, Na_ha], Na_G, Na_rev)
        Leak_I = OhmicCurr.Create(Leak[lsus], L_G, leak_rev)

#########################
# Geom setup
#########################

mesh = TetMesh.LoadAbaqus('../meshes/axon.inp', scale=1e-6)

with mesh:
    facetris = TriList([tri for tri in mesh.tris if tri.center.z == mesh.bbox.min.z])
    injverts = facetris.verts

    memb_tris = mesh.surface - facetris

    # The points along (z) axis at which to record potential
    pot_pos = np.arange(mesh.bbox.min.z, mesh.bbox.max.z, 10e-6)
    pot_tet = TetList(mesh.tets[0, 0, z] for z in pot_pos)

    cyto = Compartment.Create(mesh.tets)
    patch = Patch.Create(memb_tris, cyto, None, ssys)

    # Create the membrane across which the potential will be solved
    membrane = Membrane.Create([patch])

#########################
# Simulation setup
#########################

rng = RNG('mt19937', 512, 1234)

partition = LinearMeshPartition(mesh, 1, 1, MPI.nhosts)

sim = Simulation('TetOpSplit', model, mesh, rng, True, partition)

rs = ResultSelector(sim)

NaCurrs = rs.TRIS(memb_tris).VGNaC_I.I
KCurrs = rs.TRIS(memb_tris).VGKC_I.I
CellPot = rs.TETS(pot_tet).V

NaCurrs.metaData['trizpos'] = [tri.center.z for tri in memb_tris]
KCurrs.metaData['trizpos'] = [tri.center.z for tri in memb_tris]

NaCurrs.metaData['triarea'] = [tri.Area for tri in memb_tris]
KCurrs.metaData['triarea'] = [tri.Area for tri in memb_tris]

CellPot.metaData['tetzpos'] = pot_pos

sim.toSave(NaCurrs, KCurrs, CellPot, dt=DT_sim)

#########################
# Run simulation
#########################

with HDF5Handler('Efield_MPI') as hdf:
    sim.toDB(hdf, 'TetOpSplitSim')

    sim.newRun()

    # Inject channels
    surfarea = sim.patch.Area

    for state in VGNaC:
        prop = Na_facs[state.Count(Na_ha)][state.Count(Na_mo)]
        sim.patch.VGNaC[state].Count = Na_ro * surfarea * prop

    for state in VGKC:
        prop = K_facs[state.Count(Ko)]
        sim.patch.VGKC[state].Count = K_ro * surfarea * prop

    sim.patch.Leak[lsus].Count = L_ro * surfarea

    # Set dt for membrane potential calculation to 0.01ms
    sim.EfieldDT = 1.0e-5

    # Initialize potential to -65mV
    sim.membrane.Potential = -65e-3

    # Set capacitance of the membrane to 1 uF/cm^2 = 0.01 F/m^2
    sim.membrane.Capac = 1.0e-2

    # Set resistivity of the conduction volume to 100 ohm.cm = 1 ohm.meter
    sim.membrane.VolRes = 1.0

    # Set the current clamp
    sim.VERTS(injverts).IClamp = Iclamp/len(injverts)

    # Run the simulation
    sim.run(ENDT)